This seems to be a topic that repeatedly challenges A-level Maths students in their AS year. Often, not enough time is spent really thinking about what the discriminant reveals. This short article will hopefully lay it all out clearly.
What is it? Simply, it is \(b^{2}-4ac\). This is a function of the coefficients of a quadratic in general form \(ax^2+bx+c=0\). The discriminant is a tool that helps to know the properties of the roots/solutions without having to calculate them. Most students either were not taught or don't know where it comes from. It comes from the quadratic formula, and if you haven't had it explained before, the quadratic formula is the completed square form, with \(x\) the subject, of the general form for a quadratic \[x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\]It's a good test of your completing the square skills to see whether you can work it through to obtain the quadratic formula.
At GCSE you were hopefully taught to use the quadratic formula to find roots/solutions to a quadratic function if you can't factorise it, but you were not likely taught anything else about it. Just another formula to remember. If we take a closer look there is more to glean.
As said before, it gives us roots/solutions to our general form of the quadratic, which is dependent on the values of \(a\), \(b\) and \(c\). Further inspection shows the value of \(x\) depends on the square root term which has two possible values that come from the \(\pm\) sign. Possible, because it is limited by the value of the terms inside the square root. These terms, \(b^2-4ac\) (the discriminant), are the overall cause of the properties of the roots/solutions to the quadratic. By looking generally at the values of the discriminant, and general because we don't have any actual numbers, we can arrive at an understanding of the properties of the roots/solutions. There are three possible outcomes for the value of the discriminant, which in turn create the possible roots/solutions/values of \(x\):
- If \(b^2-4ac>0\) the value of the square root will be positive, which in turn means the \(\pm\) sign is included in the overall evaluation of \(x\). Therefore, \(x\) has two real solutions.
- If \(b^2-4ac=0\) the value of the square root is zero, leaving the term \(\frac{-b}{2a}\) . So there can be only one real solution for \(x\). This is also known as a repeated root.
- If \(b^2-4ac<0\) then we will have to evaluate square root a negative number. We are all told, perhaps up until this point in our maths education, that you can't take a square root of a negative number. The answer is true in the context of what you have learnt so far, which is that you can't make a negative number by multiplying a negative real number by itself. You may not have heard of a real number, but this is likely because there has been no context for it. The real number is contrasted with the complex number, which is a number that you can multiply by itself to make a negative number. This created a whole new branch of mathematics, complex number theory, in order to be able to solve problems that can't only be solved with real numbers. So in this case, although we can't evaluate the square root of a negative number, our square root is still evaluated with the \(\pm\) sign. So the solution to \(x\) also has two solutions. However, they are not real numbers but complex numbers. And so, we say that \(x\) has two complex roots/solutions.
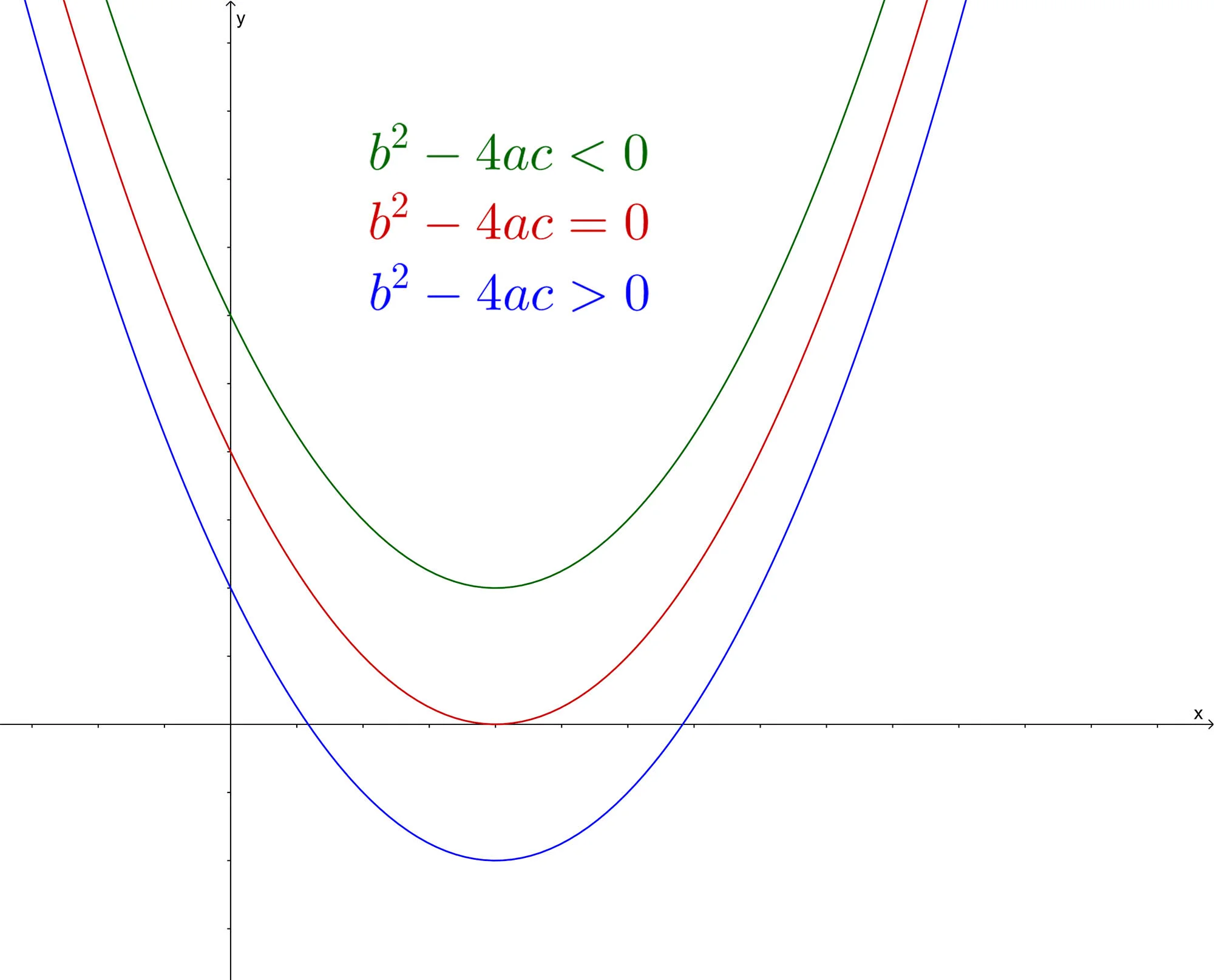
Whilst we're here, it's worth having a look at what each of these cases will look like graphically. The roots/solutions are the \(x\)-values of the function where it crosses the \(x\)-axis, or alternatively, when \(y=0\).
- You may be inclined to think that when the quadratic goes below the \(x\)-axis (blue curve) that \(b^{2}-4ac<0\). Have a closer look. When the quadratic is below the \(x\)-axis there a clearly two points where the function crosses the \(x\)-axis, therefore there are 2 distinct real roots i.e. \(b^{2}-4ac>0\).
- For the graph of the function that only touches the \(x\)-axis in one place (red curve), the answer should be obvious, it correlates to \(b^{2}-4ac=0\), one real solution or a repeated root.
- And when the curve does not touch the \(x\)-axis (green curve) there can be no solutions/roots, which correlates with \(b^{2}-4ac<0\), complex roots/solutions
When looking at a graph, think of how many solutions you see and reference those with either of the three discriminant cases and you will be spot on. Don't make the mistake of correlating the discriminant with whether the curve is above or below the \(x\)-axis.